Leetcode日记(二)

贪心算法

LeetCode376: 最长摆动序列

动态规划:每次选取最大值： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public int wiggleMaxLength(int[] nums) {
        if (nums.length == 1) return 1;
        int lastNum = 0;
        lastNum = nums[0];
        int k = 1;
        boolean flag;//是否是上坡
        boolean newflag;
        int[] dp = new int[nums.length];
        dp[0] = 1;
        while (k < nums.length && nums[k] == nums[0]) {
            dp[k] = 1;
            k++;
        }
        if (k == nums.length) return 1;
        dp[k] = 2;
        flag = nums[k] > lastNum ? true : false;
        lastNum = nums[k];
        for (int i = k + 1; i < dp.length; i++) {

            if (nums[i] == lastNum) {
                dp[i] = dp[i - 1];
            } else {
                newflag = nums[i] > lastNum ? true : false;
                if (newflag == flag) {
                    lastNum = nums[i];
                    dp[i] = dp[i - 1];
                } else {
                    flag = newflag;
                    lastNum = nums[i];
                    dp[i] = dp[i - 1] + 1;
                }

            }
        }
        return dp[nums.length - 1];
    }

来点更简洁的dp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int wiggleMaxLength(int[] nums) { 
   int[][] dp = new int[nums.length][2];// 截至nums[i]的最长摆动序列dp[i][0]表征当前处于上升态，dp[i][1]表征当前处于下降态
   dp[0][0] = 1;
   dp[0][1] = 1;
   for (int i = 0; i < nums.length; i++) {
       dp[i][0] = 1;
       dp[i][1] = 1;
       for (int j = 0; j < i; j++) {
           if (nums[i] > nums[j]) {
               dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
           } else if (nums[i] < nums[j]) {
               dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
           }
       } 
   }
   return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
}

LeetCode45: 跳跃游戏Ⅱ

能用dynamic programming尽量不用贪心算法: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int jump(int[] nums) {
        int max = 0;
        int[] dp = new int[nums.length];
        dp[0] = 0;
        for (int i = 0; i <= max; i++) {
            int newMax = Math.max(nums[i] + i, max);
            if (newMax > max) {
                for (int j = max + 1; j <= newMax && j < nums.length; j++) {
                    dp[j] = dp[i] + 1;
                }
                max = newMax;
                if (max >= nums.length - 1) break;
            }

        }
         return dp[nums.length - 1];
    }

回溯算法

LeetCode77: 组合优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private List<List<Integer>> result = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
          backtracking(n, k, 1);
          return result;
    }

    private void backtracking(int n, int k, int startindex) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startindex; i <= n - (k - path.size()) + 1; i++) {
            path.add(i);
            backtracking(n, k, i + 1);
            path.removeLast();
        }
    }

LeetCode:组合总和III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private List<List<Integer>> result = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k, n, 1, 0);
        return result;
    }

    private void backtracking(int k, int target, int startindex, int sum) {
        if (sum > target) return;
        if (path.size() == k) {
            if (target == sum) result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startindex; i <= 9; i++) {
            sum += i;
            path.add(i);
            backtracking(k, target, i + 1, sum);
            sum -= i;
            path.removeLast();
        }
    }

LeetCode17: 电话号码的组合数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
private List<String> result = new ArrayList<>();
    private StringBuilder sb = new StringBuilder();

    private HashMap<Integer, String> hp = new HashMap<>();

    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return result;
        }
        hp.put(2, "abc");
        hp.put(3, "def");
        hp.put(4, "ghi");
        hp.put(5, "jkl");
        hp.put(6, "mno");
        hp.put(7, "pqrs");
        hp.put(8, "tuv");
        hp.put(9, "wxyz");
        backtracking(digits);
        return result;
    }

    private void backtracking(String digits) {
        if ("".equals(digits)) {
            result.add(sb.toString());
            return;
        }
        int i = digits.charAt(0) - '0';
        String s = hp.get(i);
        for (int j = 0; j < s.length(); j++) {
            sb.append(s.charAt(j));
            backtracking(digits.substring(1, digits.length()));//递归
            sb.deleteCharAt(sb.length() - 1);//回溯
        }

    }

LeetCode39: 组合总和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private List<List<Integer>> result = new ArrayList<>();
    //private List<Integer> path = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0, 0);
        return result;
    }

    private void backtracking(int[] candidates, int target, int sum, int startIndex) {
        if (sum > target) return;
        if (sum == target) {
            System.out.println(path);
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) {
            sum += candidates[i];
            path.add(candidates[i]);
            backtracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }

LeetCode40: 组合总和Ⅱ

这里需要考虑到提前清除重复选择，而且重复选择是在树的同层被清除的: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
private List<List<Integer>> result = new ArrayList<>();

    private LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        boolean[] used = new boolean[candidates.length];
        backtracking(candidates, target, 0, 0, used);
        return result;
    }

    private void backtracking(int[] candidates, int target, int sum, int startIndex, boolean[] used) {
        if (target == sum) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
            if (i >= 1 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
            used[i] = true;
            path.add(candidates[i]);
            sum += candidates[i];
            backtracking(candidates, target, sum, i + 1, used);
            used[i] = false;
            sum -= candidates[i];
            path.removeLast();
        }
    }

LeetCode131: 分割回文串

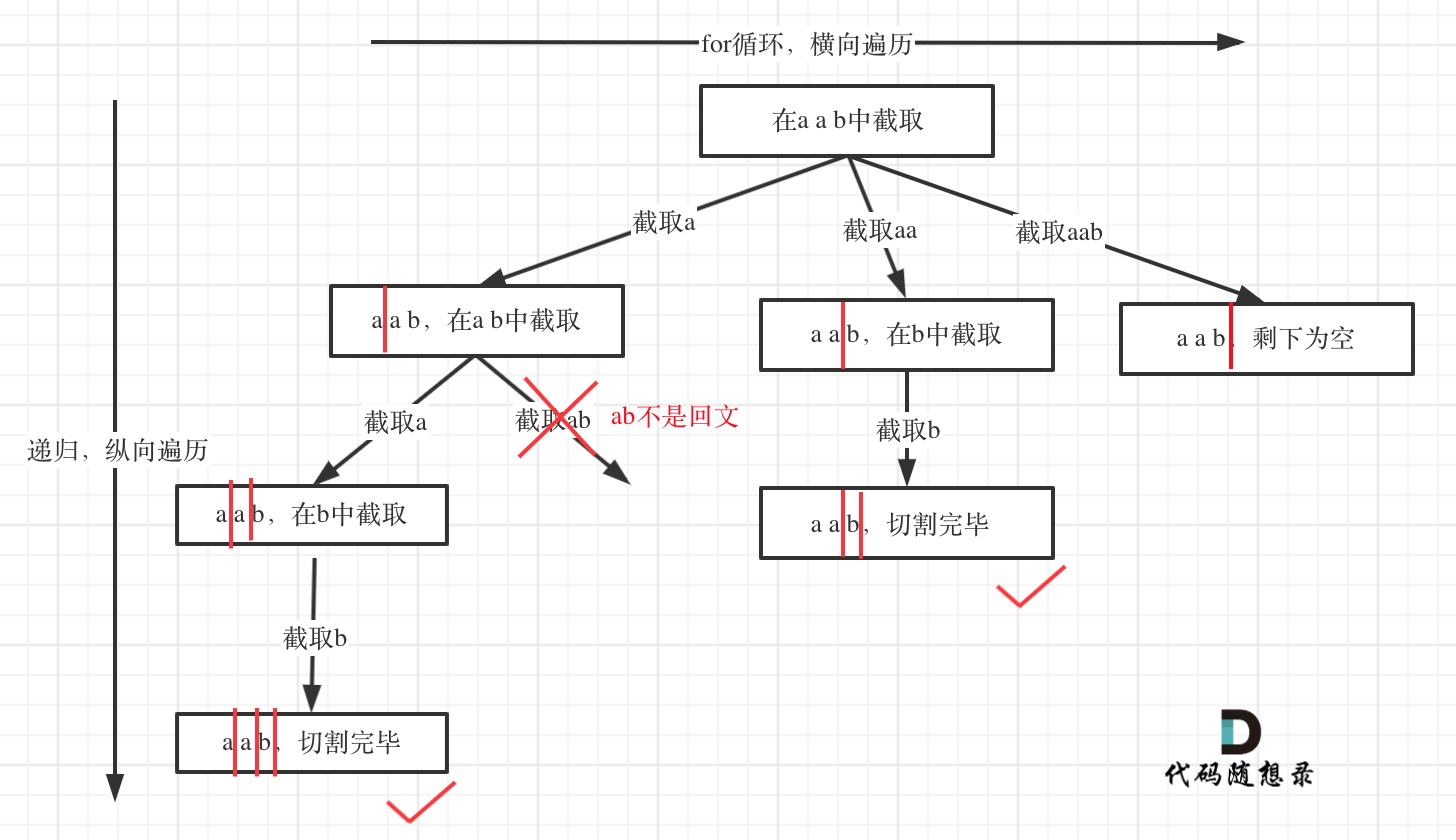
对于这个树形结构 for循环是同一次切割

回溯算法树形图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
private List<List<String>> result = new ArrayList<>();

private LinkedList<String> path = new LinkedList<>();

public List<List<String>> partition(String s) {
    backtracking(s, 0);
    return result;
}

private void backtracking(String s, int startIndex) {
    if (startIndex >= s.length()) {
        result.add(new ArrayList<>(path));
        return;
    }
    for (int i = startIndex; i < s.length(); i++) {
        if (isPalindrome(s.substring(startIndex, i + 1))) {
            path.add(s.substring(startIndex, i + 1));
        } else {
            continue;
        }
        backtracking(s, i + 1);
        path.removeLast();
    }
}

private boolean isPalindrome(String str) {
    for (int i = 0, j = str.length() - 1; i < j; i++, j--) {
        if (str.charAt(i) != str.charAt(j)) return false;
    }
    return true;
}

LeetCode93: 复原IP地址

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
private List<String> result = new ArrayList<>();
   private LinkedList<Integer> path = new LinkedList<>();

   public List<String> restoreIpAddresses(String s) {
       if (s.length() > 12 && s.length() < 4) return result;
       backtracking(s, 0);
       return result;
   }

   private void backtracking(String s, int startIndex) {
       if (path.size() == 3) {
           String s1 = s.substring(startIndex, s.length());
           if (s1.length() > 1 && s1.charAt(0) == '0' || s1.length() == 0 || s1.length() > 3) {
               return;
           }
           Integer i = Integer.parseInt(s1);
           if (i > 255) return;
           path.add(i);
           StringBuilder sb = new StringBuilder();
           for (Integer integer : path) {
               sb.append(integer);
               sb.append(".");
           }
           sb.delete(sb.length() - 1, sb.length());
           result.add(sb.toString());
           path.removeLast();
           return;
       }
       for (int i = startIndex; i < s.length(); i++) {
           String s1 = s.substring(startIndex, i + 1);
           if (s1.length() > 1 && s1.charAt(0) == '0' || s1.length() == 0 || s1.length() > 3) {
               break;
           }
           if (Integer.parseInt(s1) > 255) break;
           path.add(Integer.parseInt(s1));
           backtracking(s, i + 1);
           path.removeLast();

       }

   }

LeetCode90: 子集II

在LeetCode78的基础上，增加了去重的操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
private List<List<Integer>> result = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();


    public List<List<Integer>> subsetsWithDup(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.sort(nums);
        backtracking(nums, 0, used);
        return result;
    }

    private void backtracking(int[] nums, int startIndex, boolean[] used) {
        result.add(new ArrayList<>(path));
        if (startIndex >= nums.length) {
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            if ( i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.removeLast();
        }
    }

LeetCode491: 递增子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private List<List<Integer>> result = new ArrayList<>();
private LinkedList<Integer> path = new LinkedList<>();

public List<List<Integer>> findSubsequences(int[] nums) {
    backtracking(nums, 0);
    return result;
}

private void backtracking(int[] nums, int startIndex) {
    if (path.size() >= 2) result.add(new ArrayList<>(path));
    HashSet<Integer> hs = new HashSet<>();
    for (int i = startIndex; i < nums.length; i++) {
        if (path.size() > 0 && nums[i] < path.getLast() || hs.contains(nums[i])) {
            continue;
        }
        path.add(nums[i]);
        hs.add(nums[i]);
        backtracking(nums, i + 1);
        path.removeLast();
    }

    }

LeetCode47: 全排列Ⅱ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private List<List<Integer>> result = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();
    private HashSet<Integer> hs = new HashSet<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
            backtracking(nums, 0);
            return result;
    }

    private void backtracking(int[] nums, int startIndex) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        HashSet<Integer> ht = new HashSet<>();
        for (int i = startIndex; i < nums.length; i++) {
            if (hs.contains(i) || ht.contains(nums[i])) {
                continue;
            }
            path.add(nums[i]);
            hs.add(i);
            ht.add(nums[i]);
            backtracking(nums, startIndex);
            hs.remove(i);
            path.removeLast();
        }
    }

不使用set，改为使用used数组处理，速度更快:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private List<List<Integer>> result = new ArrayList<>();
    private LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.sort(nums);
        backtracking(nums, used);
        return result;
    }

    private void backtracking(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (used[i] == true || i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
            path.add(nums[i]);
            used[i] = true;
            backtracking(nums, used);
            used[i] = false;
            path.removeLast();
        }
    }

总的来说，在同一层数量去重就是在循环内部处理，在同一树枝去重就是在递归函数这一级别处理。

LeetCode51: N皇后问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
private List<List<String>> result = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backtracking(n, 0, chessboard);
        return result;
    }

    private void backtracking(int n, int row, char[][] chessboard) {
        if (row == n) {
            result.add(Array2List(chessboard));
            return;
        }
        for (int col = 0; col < n; col++) {
            if (isValid(row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backtracking(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }

    private boolean isValid(int row, int col, int n, char[][] chessboard) {
        //检查列
        for (int i = 0; i < row; i++) {
            if (chessboard[i][col] == 'Q') return false;
        }
        // 检查45度对角线
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // 检查135度对角线
        for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }

    private List<String> Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();
        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }

回溯算法总结

回溯算法能解决如下问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 棋盘问题：N皇后，解数独等等

组合问题

for循环横向遍历，递归纵向遍历，回溯不断调整结果集

切割问题

同组合问题解决，如果想到了用求解组合问题的思路来解决 切割问题本题就成功一大半。

子集问题

注意去重方式，用hash表还是used数组。

棋盘问题

N皇后问题。

栈和队列

LeetCode232: 用栈实现队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class MyQueue {
    private Stack<Integer> stackIn;
    private Stack<Integer> stackOut;
    public MyQueue() {
        stackIn = new Stack<>();
        stackOut = new Stack<>();
    }

    public void push(int x) {
        stackIn.push(x);
    }

    public int pop() {
        if (stackOut.isEmpty()) {
            while (!stackIn.isEmpty()) {
                stackOut.push(stackIn.pop());
            }
            return stackOut.pop();
        } else {
            return stackOut.pop();
        }
    }

    public int peek() {
        if (stackOut.isEmpty()) {
            while (!stackIn.isEmpty()) {
                stackOut.push(stackIn.pop());
            }
            return stackOut.peek();
        } else {
            return stackOut.peek();
        }
    }

    public boolean empty() {
        return stackOut.isEmpty() && stackIn.isEmpty();
    }
}

LeetCode225: 用队列实现栈

双队列法: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MyStack {
    //作为主要的队列，其元素排列顺序和出栈顺序相同
    private Queue<Integer> queueIn;
    //仅作为临时放置
    private Queue<Integer> queueData;

    public MyStack() {
        queueIn = new LinkedList<>();
        queueData = new LinkedList<>();
    }

    public void push(int x) {
        while (!queueIn.isEmpty()) {
            queueData.offer(queueIn.poll());
        }
        queueIn.offer(x);
        while (!queueData.isEmpty()) {
            queueIn.offer(queueData.poll());
        }
    }

    public int pop() {
        return queueIn.poll();
    }

    public int top() {
        return queueIn.peek();
    }

    public boolean empty() {
        return queueIn.isEmpty();
    }
}

单队列法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MyStack {
    private Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    public void push(int x) {
        int size = queue.size();
        queue.offer(x);
        while (size > 0) {
            queue.offer(queue.poll());
            size--;
        }
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

LeetCode347: 前K个高频元素

优先级队列： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int[] topKFrequent(int[] nums, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2)-> o1[1] - o2[1]);
        HashMap<Integer, Integer> hp = new HashMap<>();
        int[] result = new int[k];
        for (int num : nums) {
            if (hp.containsKey(num)) {
                hp.put(num, hp.get(num) + 1);
            } else {
                hp.put(num, 1);
            }
        }
        for (Map.Entry<Integer, Integer> entry : hp.entrySet()) {
            int[] tmp = new int[2];
            tmp[0] = entry.getKey();
            tmp[1] = entry.getValue();
            pq.offer(tmp);
            if (pq.size() > k) {
                pq.poll();
            }
        }
        for (int i = 0; i < k; i++) {
            result[i] = pq.poll()[0];
        }
        return result;
    }

LeetCode239: 滑动窗口最大值

此题核心在于构造单调队列，保障从单调队列中peek的元素是最大值，对于offer操作，若入口有更小的，全部remove，对于poll，只有移除的值与peek相同，才poll掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        MyQueue myQueue = new MyQueue();
        int[] result = new int[nums.length - k + 1];
        int i = 1, j = k;
        for (int l = 0; l < k; l++) {
            myQueue.offer(nums[l]);
            result[0] = myQueue.peek();
        }
        for (; j < nums.length; i++, j++) {
            myQueue.poll(nums[i - 1]);
            myQueue.offer(nums[j]);
            result[i] = myQueue.peek();
        }
        return result;
    }
}
class MyQueue {
    Deque<Integer> deque ;

    public MyQueue() {
        deque = new LinkedList<>();
    }

    //弹出元素时，比较当前要弹出的数值是否等于队列出口的数值，如果相等则弹出
    //同时判断队列当前是否为空
    void poll(int val) {
        if (!deque.isEmpty() && val == deque.peek()) {
            deque.poll();
        }
    }
    void offer(int val) {
        while (!deque.isEmpty() && val > deque.getLast()) {
            deque.removeLast();
        }
        deque.offer(val);
    }
    //队列队顶元素始终为最大值
    int peek() {
        return deque.peek();
    }
}

单调栈

LeetCode739:每日温度

单调栈原始写法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int[] dailyTemperatures(int[] temperatures) {
        int[] resuls = new int[temperatures.length];
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < temperatures.length; i++) {
            if (stack.isEmpty()) {
                stack.push(i);
            } else {
                if (temperatures[i] <= temperatures[stack.peek()]) {
                    stack.push(i);
                } else {
                    while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                        Integer pop = stack.pop();
                        resuls[pop] = i - pop;
                    }
                    stack.push(i);
                }
            }
        }
        return resuls;
    }

单调栈简化写法：

1
2
3
4
5
6
7
8
9
10
11
12
public int[] dailyTemperatures(int[] temperatures) {
        int[] resuls = new int[temperatures.length];
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < temperatures.length; i++) {
            while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                Integer pop = stack.pop();
                resuls[pop] = i - pop;
            }
            stack.push(i);
        }
        return resuls;
    }

LeetCode503: 下一个更大元素Ⅱ(循环版本）

遍历两遍: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int[] nextGreaterElements(int[] nums) {
        Stack<Integer> stack = new Stack<>();
        int[] result = new int[nums.length];
        for (int i = 0; i < result.length; i++) {
            result[i] = -1;
        }
        for (int i = 0; i < nums.length; i++) {
            while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
                result[stack.peek()] = nums[i];
                stack.pop();
            }
            stack.push(i);
        }
        int max = nums[0], index = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > max) {
                max = nums[i];
                index = i;
            }
        }
        for (int i = index + 1;(i - nums.length) <= index; i++) {
            while (!stack.isEmpty() && nums[i % nums.length] > nums[stack.peek()]) {
                result[stack.peek()] = nums[i % nums.length];
                stack.pop();
            }
            stack.push(i % nums.length);
        }
        return result;
    }

简化一下: 直接遍历长度* 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[] nextGreaterElements(int[] nums) {
        Stack<Integer> stack = new Stack<>();
        int[] result = new int[nums.length];
        for (int i = 0; i < result.length; i++) {
            result[i] = -1;
        }
        for (int i = 0; i < nums.length * 2; i++) {
            while (!stack.isEmpty() && nums[i % nums.length] > nums[stack.peek()]) {
                result[stack.peek()] = nums[i % nums.length];
                stack.pop();
            }
            stack.push(i % nums.length);
        }
        return result;
    }

LeetCode42: 接雨水

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int trap(int[] height) {
        Stack<Integer> stack = new Stack<>();
        int area = 0;
        for (int i = 0; i < height.length; i++) {
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int rightHeight = height[i];
                int nowHeight = height[stack.pop()];
                int leftHeight = 0;
                if (!stack.isEmpty()) {
                    leftHeight = height[stack.peek()];
                } else {
                    continue;
                }
                int realHeight = Math.min(rightHeight, leftHeight) - nowHeight;
                int width = i - stack.peek() - 1;
                area += realHeight * width;
            }
            stack.push(i);
        }
        return area;
    }

LeetCode84: 计算矩形最大面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int largestRectangleArea(int[] heights) {
        int[] newheights = new int[heights.length + 2];
        for (int i = 0; i < heights.length; i++) {
            newheights[i + 1] = heights[i];
        }
        Stack<Integer> stack = new Stack<>();
        int maxArea = 0;
        for (int i = 0; i < newheights.length; i++) {
            while (!stack.isEmpty() && newheights[i] < newheights[stack.peek()]) {
                int rightIndex = i;
                int height = newheights[stack.pop()];
                int leftIndex = stack.peek();
                maxArea = Math.max(maxArea, height * (rightIndex - leftIndex - 1));
            }
            stack.push(i);
        }
        return maxArea;
    }
Leetcode
#代码练习日记
Leetcode日记(二)
http://example.com/2023/10/19/LeetCode日记(二)/
作者
John Doe
发布于
2023年10月19日
许可协议